An Introduction to Mathematical Physics
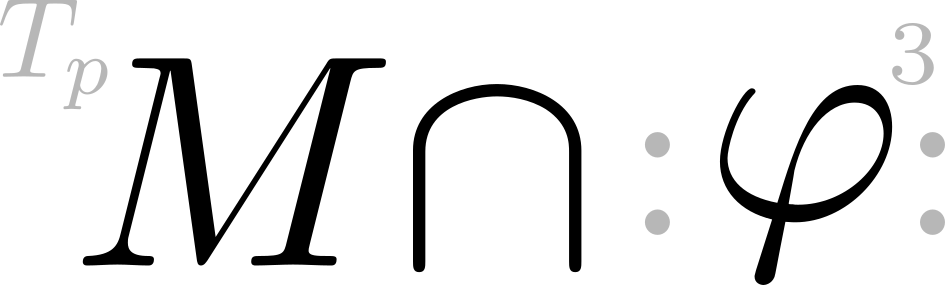
The idea of mathematical physics in any form of its meaning, is not yet spread to the (academic) masses of India. It has been quite a journey to reconcile ideas in this field, amidst this local state of affairs. Five years of multiple breakthrooughs in understanding this has finally informed my current perspective, buidling on the historical and contemporary ideas. I feel secure and stable with these currently and would like to communicate the learnings. In the hope that it will help the next cohorts of undergraduates in navigating through these tricky waters of mathematics $\times$ physics.
So, what is Mathematical Physics?
Is it about,
$\diamond$ Trying to reformulate or understand physics more rigorously?
$\diamond$ Using the more abstracct and rigorous aspects of mathematics to achieve new results in physics?
$\diamond$ Develop new structures, insights and results in Mathematics using physics?
As we will see, there have been efforts in all of these domains! How should one chase this field however, probably depends on an individual’s taste. When I first started started to appraoach academics regarding these interests, I have been asked early whether I want to cater to the interests of mathematicians or physicists. It was rather non-trivial question to answer, and I only figured it near the end of my master’s journey. However, the perspectives from multiple leaders in this field has indeed informed me and validated me on many levels.
Perspective from the leaders
We attempt to discuss general topics in such a way that the physical significance of the theory is exhibited as clearly as possible, and then to build the mathematical formalism. In doing so, we do not aim at "mathematical rigour" of exposition, which in theoretical physics often amounts to self-deception.
In the preface to their book on Quantum mechanics, Landau and Lifschitz quite beautifully admit the approach one usually takes in physics. Our goals in theoretical physics are more driven by the nature’s way than our imposition on it. We try as much as possible to replicate and predict the patterns of nature. In this process, the rigour of mathematics tends to take a side seat.
Of course, mathematics is the language of physics. But one should look at mathematics as a distinct field which precisely deals with the rigour that physics misses out. Indeed, historically much of mathematics was born out of direct interests in nature. And mathematics then occurs as a systematic study of these analytic, symmetric and geometric structures in their own right, much more elaborate than what might be required or relevant for physics.
However with the exposure in techniques or rigour of mathematics, one cannot overlook what it takes to do physics, or teach physics, when compared to more concrete nature of mathematics. And it is this difference that I think should be noted early on to be able to glide through the academic paths more securely. A highlight in this direction comes from a major academic voice - David Tong, in a podcast episode of Mindscape, hosted by Sean Carroll.
0:06:45.1: ...I guess that's true. I like cheating. That's an important part of teaching. It's figuring out what details it's important to get right and which ones you can wishy-washy a little bit. It's why teaching physics is much easier than teaching mathematics. I have taught mathematics courses. When we teach general relativity in Cambridge, we do it properly. We do differential geometry. We do it very, very rigorously. It's very hard to hide when you're teaching mathematics. Very hard. Very hard to lie. Very hard to argue by force of personality alone. In physics, that's very easy.
0:07:27.9: Just sort of push through. There's a bit of bombast. So I'm not afraid to do that when necessary.
This also reveals the possibiity of students being left unsatisfied with the rigor of physics classes, or even subject for that matter. And that those students are likely to be the handful of ones who are more mathematically inclined. It might be very tricky to balance the personality of physics with the rigor of math when teaching a course - and those minority of people must learn to stitch multuple ideas together, communicate and learn from different places to reconcile mathematical physics. That’s how my journey has been with the locally uncommon interests with little support!
What Tong pointed out is a rather remarkable feature of physics, that math might not enjoy immediately. However, I have been convinced that, it doesn’t mean math can’t be communicated with personality! It’s still possible to stitch ideas together beautifully and make seemingly convincing arguments yet less rigorous. However, such a communication occurs only in places like post-learning expositions, talks and sometimes even during class to mention some edge results beyond the scope that course – only to pass the broader ideas of the topic but not as a tool on its own to show/prove things.
Argumentation in physics, uses this personality and different ways to phrase things inspired by nature rather than rigor (which it openly misses out). This way the language of physics needs mathematics but it can’t afford to focus on the rigor, it has much more broader goals of reconciling nature in any way possible.
Arguments in physics need not inherently be backed by a formal justification. We often enter the realms of mathematics, if we try to focus more on that. But since it serves the needs of physics, it’s doesn’t seem like a reason for concern. More so because it’s the messengers between both the fields not just physicists, who enabled a huge progress in physics! So, progress in science is almost always inter-disciplinary and we can’t be too hard on either of the fields to be too narrow about their methods, as long as they serve their own purpose. I would like to recall the words of Hermann Weyl, one of the early academics who interacted between math and physics, laying out the platform for a large synergy between mathematics and physics that we enjoy today. Mathematics and Physics have been on a long self-directed paths in the 19th and early 20th centuries. But with the advent of relativity and quantum mechanics, they have been re-united in the late 1900s.
In this drama of mathematics and physics, which fertilise each other in the dark, but which prefer to deny and misconstrue each other face to face—I cannot, however, resist playing the role of a messenger, albeit, as I have abundantly learned, often an unwelcome one.
In the early and middle part of my undergrad years, I used to wish for physics to be rigorous. It is until I really understood that the goals are different, and that it’s my personal acadaemic interests to become more of a messenger between math and physics. Something that perturbed those earlier notions of mathematical physics quite uncomfortably was Ludwig Faddeev’s opinions on these matters!
The goal of a mathematical physicist is not to make rigorous what is already understood, to the extent of being true beyond reasonable doubt, by physicists, but to achieve something they could not do with physical intuition, and do it on the basis of mathematical knowledge and mathematical intuition.
I think the earlier notions of seeking rigorous physics, came from a lack of opportunity to do more mathematics, and then wishing the things I studied (mostly physics due to my major) to be more mathematical. It is not until I started my graduate part of the degree, studying quantum field theory and general relativity that I got more opportunities to engage in mathematics especially in the area of geometry, due to their deep interactions!
There are many instances which motivated me a lot towards pure mathematics. Some instances relate to the following,
We stated above that $\nabla \times E = 0$ is equivalent to writing $E = - \nabla\phi$. This is true when space is $R^3$ or, in fact, if we take space to be any open ball in $R^3$. But if our background space has a suitably complicated topology then there are solutions to $\nabla \times E = 0$ which cannot be written in the form $E = - \nabla\phi$. This is tied ultimately to the beautiful mathematical theory of de Rham cohomology. Needless to say, in this starter course we’re not going to worry about these issues. We’ll always take spacetime to have topology $R^4$ and, correspondingly, any spatial hypersurface to be $R^3$.
Particles are irreducible representations of the Poincare group.
...This formula is so fundamental to the subject that one might almost say electrostatics is the study of Laplace’s equation. At the same time, it is a ubiquitous equation, appearing in such diverse branches of physics as gravitation and magnetism, the theory of heat, and the study of soap bubbles. In mathematics it plays a major role in analytic function theory. To get a feel for Laplace’s equation and its solutions (which are called harmonic functions), we shall begin with the one and two-dimensional versions, which are easier to picture and illustrate all the essential properties of the three-dimensional case (though the one-dimensional example lacks the richness of the other two).
It is through instance as basics as these and many many more, I realized I am more interested in exploring mathematical structures. The connections in math and physics have of course evolved from the days of Newton to Witten. Our next goal is to describe these historical and contemporary ideas.
Directions in Mathematical Physics
A history
Newton, Leibniz - preCM
Bernoulli - Fluids
Langrange - CM
Poincare
Hilbert
Neumann
Einstein
Dirac
Weyl, Wigner
Chern, Whitney (Yang)
Witten, Atiyah, Donaldson
String Theory
Current Research
(Quantum) Algebra, Geometry and Topology. TQFTs, Low-dimensional topology, Gauge Theory, (Homological) Mirror Symmetry, Symplectic Geometry, Geometric/Deformation Quantization, Quantum groups, $C^*$ algebras, Operator Algebras and CFT, Representation theory.