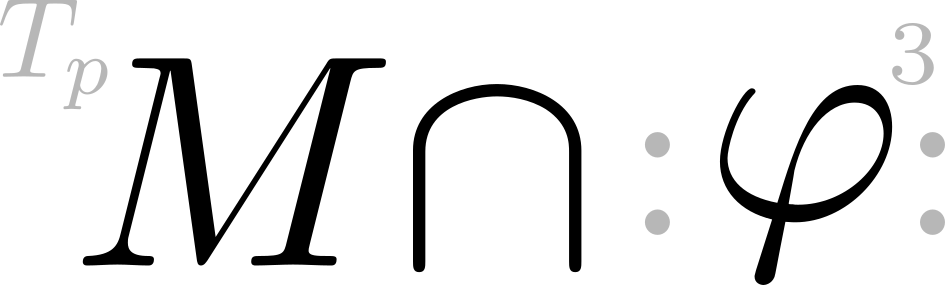An Introduction to Mathematical Physics

On the Geometry of Curves and Surfaces

This semester, I took a course on the geometric theory of curves and sufaces, which are basically now refered to as the classical aspects of (differential) geometry. This is a post to put things in perspective. I want to pick out the essentials of the course, and form a narrative around this subject.

Celebrating Quantum Field Theory

Back when I was in second and third years here at NISER, I found the idea of Quantum Field Theory quite exciting and was looking forward to get to know how all the fundamental stuff is calculated. I think much of the longing came from the book Surely you are joking Mr. Feynman. I wished for someone to just talk about it and pass the feels. Of course David Tong did, and I was waiting to see the calculations myself. Of course, I was no way ready until this semester to understand such calculations, but you get it. I was excited, and also patient. And today we finished calculating the anomalous magnetic moment! Yes, for which Schwinger was awarded the 1965 Nobel Prize, and is one of the most accurate theoretical and experimental agreement in the history of phyiscs. I am elated and I want to celebrate this with a series of articles on some fundamental QFT results, that could probably keep the excitement high for the studfents in their junior years. I want to do this atleast for my third year self.

Hydrogen Atom - The final take?

The study of atoms is a mysterious one, especially when one begins to study this in high school, hearing the abstract concepts of wavefunctions and probability. In a first course on Quantum Mechanics one finally tackles this atom rigorously - as the most simple spherically symmetric system and also as a rare example to solve exactly. In this article we uncover some more secrets about this atom. High resolution spectrometers observed a fine splitting over the degeneracy one is familiar with from high school. What follows is a story about this more richer and broken energy structure.