Riemann Integrability

Hyping Riemanna-Stieltjes Integral.

We now enter the second pillar of calculus – Integration, which takes a slightly different route from what we are used to in continuity and differentiation. In particular, it builds more directly on the completion of reals, rather than a sequences of limits. Our efforts would essentially give us a rigorous formulation of the intuitive area approach to Integration. This involves four main ingredients:

Partition of an interval.
Size of intervals.
Simplest integrable objects which can also approximate functions in a partition.
Shrinking the fuzz of such an approximation.

Parition & Length

Here we deal only with bounded intervals. And the length of these is defined in an obvious way.

If $I$ is a bounded interval, we define the length of $I$ to be the difference $\left| I \right| := b-a$; where $I$ occurs as $\left[ a,b \right], (a,b),(a,b],[a,b)$.

And the parition of a bounded interval $I$ is a finite set $\mathbf{P}$ of bounded intervals contained in $I,$ such that every $x \in I$ lies exactly in one of the bounded intervals $J$ in $\mathbf{P}.$

Of course these partitions are pretty intuitive, we are basically chopping the intervals in different ways. However note that, aprirori we are not restricting this partitions to have their intervals be as small as possible. But our eventual goal would indeed be to work on paritions which reduces the fuzz of the approximation in any given interval. However we won’t make this explicit. It simply amounts to taking an infimum or supremum over different paritions on which integration is done using the simple objects.

One of the properties of these partitions that make many operations well behaved is their additive nature.

Let $I$ be a bounded interval and let $\mathbf{P}$ be a partition of $I$ of cardinality $n$. Then $$ \left| I \right| = \sum_{J\in \mathbf{P}} \left| J \right|.$$

Induct over $n$ and when both $b \in I, b\not\in I$ find $K \in \mathbf{P}$ and $I\setminus K \in \mathbf{P}$ whose lengths sum to $|I|$ and use the inductive hypothesis over $\left| I-K \right|$ to finish the proof.

We can also give the finer and coarser notions of a parition in comparision to other partitions. And most importantly we can have a common refinement.

Let $\mathbf{P},\mathbf{P'}$ be two paritions of $I$. Then The common refinement $\mathbf{P}\# \mathbf{P'}$ of $\mathbf{P}$ and $\mathbf{P'}$ is the set, $$ \mathbf{P}\# \mathbf{P'} = \left\{K\cap J: K \in \mathbf{P} \text{ and } J \in \mathbf{P'}\right\}$$ which indeed turns out be a parition.

Most simple Integrable objects

We now deal with piecewise constant functions in the sense that there is a parition $\mathbf{P}$ of $I$ on which the function is defined to be constant over each $J \in \mathbf{P}.$ Note that these are closed unders imple algebraic operations.

We can now define the most primitive notion of integration of functions.

Let $f:I \to \mathbb{R}$ be a function which is pievevwise constant with respect to $\mathbf{P}$ a parition of $I$. Then we define the piecewise constant integeral $p.c. \int_{[\mathbf{P}]}f$ of $f$ with respect to the parition $\mathbf{P}$ by $$ p.c. \int_{[\mathbf{P}]} f = \sum_{J\in \mathbf{P}} c_J\left| J \right| $$ where for each $J \in \mathbf{P}$, $c_J$ is the constant value of $f$ on $J.$

This reflects the simple case of summing areas of rectangles formed by the piecewise constant functions. The existence of the refinement of two paritions ensure that this integral is invariant under the change of partitions! Basically one can easily show that the sum over a partition equals the sum over a refinement with other partition! This is where the additive nature of interval lengths becomes really important. We can split a constant function firther into it’s refinement, without any hastle.

We can now realise some basic properties of this integral, which also follow for furture integral formulations.

(Laws of Integration) Let $I$ be a bounded interval, and let $f : I \to \mathbf{R}$ and $g : I \to \mathbf{R}$ be piecewise constant functions on $I$.

a) We have $p.c. \int_I (f + g) = p.c. \int_I f + p.c. \int_I g$.
b) For any real number $c$, we have $p.c. \int_I (cf) = c(p.c. \int_I f)$.
c) We have $p.c. \int_I (f - g) = p.c. \int_I f - p.c. \int_I g$.
d) If $f(x) \ge 0$ for all $x \in I$, then $p.c. \int_I f \ge 0$.
e) If $f(x) \ge g(x)$ for all $x \in I$, then $p.c. \int_I f \ge p.c. \int_I g$.
f) If $f$ is the constant function $f(x) = c$ for all $x$ in $I$, then $p.c. \int_I f = c|I|$.
g) Let $J$ be a bounded interval containing $I$ (i.e., $I \subseteq J$), and let $F : J \to \mathbf{R}$ be the function $$F(x) := \begin{cases} f(x) & \text{if } x \in I \\ 0 & \text{if } x \notin I \end{cases}$$ Then $F$ is piecewise constant on $J$, and $p.c. \int_J F = p.c. \int_I f$.
h) Suppose that $\{J, K\}$ is a partition of $I$ into two intervals $J$ and $K$. Then the functions $f|_J : J \to \mathbf{R}$ and $f|_K : K \to \mathbf{R}$ are piecewise constant on $J$ and $K$ respectively, and we have $$p.c. \int_I f = p.c. \int_J f|_J + p.c. \int_K f|_K.$$

Parts $(g), (h)$ are fun to prove :). Now that we have developed the core ingredients, we can go further.

Part II: Riemann Integration

Two ingredients go into this formulation.

Approximating the integral of a general function through piecewise functions.
Demanding the fuzziness of this approximation to be as less as possible.

This approximating manifests from both sides, by seeking piecewise constant integrals of functions which majorize and minorize the original function.

Let $f:I\to \mathbb{R}$ be a bounded function defined on a bounded interval $I$. We define the ipper Riemann integral $\overline{\int}_ I f$ by $$\overline{\int}_ I f = inf \left\{p.c. \int_I g : g \text{ is a p.c. function on $I$ s.t. } g(x) \ge f(x) \forall x \in I \right\}$$ and the \textit{lower Riemann integral} $\overline{\int}_ I f$ by the formula $$ \underline{\int}_ I f = sup \left\{p.c. \int_ I g: g \text{ is a p.c. function on $I$ s.t. } g(x) \le f(x) \forall x \in I\right\}.$$

We had hyped about demanding the fuzziness to be as less as possible, but the situation in truth is on the other side, where we define the integral to be precisely the smallest possible fuzziness when the interval and the function together are being replaced by more simple objects ($p.c. \int _ I g$).

Now, it is very easy to note the following bound on the lower and upper integrals!

\[-M\left| I \right| \le \underline{\int}_ I f \le \overline{\int}_ I f \le M \left| I \right|\]

where $f$ is bounded by $M$ in $I$. Now we can define what it means to be Riemann integrable by making use of these two sides\ldots

Let $f:I \to \mathbb{R}$ be a bounded function on a bounded interval $I.$ If $\underline{\int}_ I f = \overline{\int}_ f$, then we say that $f$ is Riemann integrable on $I$ and define, $$ \int_ I f = \underline{\int}_ I f = \overline{\int}_ f.$$

This precisely mimics the $lim\ sup, lim\ inf$ dynamics! It is very clear that the piecewise constant functions are Riemann integrable with $\int_I f = p.c. \int_I f$! Because, the majorization and minorization of $f$ are trivial viz. itself.

This whole procedure infact is equivvalent to the taking upper and lower sums of the function through a partition weighted by the lengths of the intervals of that parition. We can then supress the fuzz by taking an infimum of the upper sum and supremum of the lower sum over the possible paritions to define the result as a Riemann Integral. This boils down to the previous integrability condition, because asking for the extremal bounds of the lower-uppersums or integrals, at every point, the notion of constant function, the smallest interval containing it (related to the parition) and the maximum/minimum of the function in that interval fuse together to give the same meaning!

To put this rigorously, first define the upper and lower sums:

Let $f : I \to \mathbf{R}$ be a bounded function on a bounded interval $I$, and let $\mathbf{P}$ be a partition of $I$. We define the upper Riemann sum $U(f, \mathbf{P})$ and the lower Riemann sum $L(f, \mathbf{P})$ by $$U(f, \mathbf{P}) := \sum_{J \in \mathbf{P} : J \neq \emptyset} (\sup_{x \in J} f(x))|J|$$ and $$L(f, \mathbf{P}) := \sum_{J \in \mathbf{P} : J \neq \emptyset} (\inf_{x \in J} f(x))|J|.$$

We now show the connection to previous notion of integrability. The following relation between sums and integrals follows quite easily for a parition $\mathbf{P}$ with respect to which $h,g$ minorize and majorize $f$ respectively.

\[p.c.\int_I h \le L\left( f,\mathbf{P} \right) \le U\left( f,\mathbf{P} \right) \le p.c. \int_I g.\]

In particular, for any parition $\mathbf{P}$,

\[p.c.\int_I g \ge U\left( f,\mathbf{P} \right) \ge inf(U).\]

So, $inf(U)$ is a lower bound to the all the p.c integrals of functions majorizing $f$! Infact it follows that this is a greatest lower bound. Because any upper sum $K > inf(U)$ would automatically give a p.c. function (and thus an integral) which lies between $K$ and $inf(U)$! This shows no $K > inf(U)$ is a lower bound to $p.c \int_I g$, $g$ majorizing $f$! Similar proof shows $sup(L)$ is the least upper bound to $p.c. \int_I h$, $h$ minorizing $f$!

This puts Riemann sums and integrability on an equal footing,

Let $f : I \to \mathbf{R}$ be a bounded function on a bounded interval $I$. Then $$ \overline{\int_I} f = \inf\{U(f,\mathbf{P}) : \mathbf{P} \text{ is a partition of } I\} $$ and $$ \underline{\int_I} f = \sup\{L(f,\mathbf{P}) : \mathbf{P} \text{ is a partition of } I\} $$

So Riemann integrability indeed amounts to ask the paritions we require more succintly. Although, we only require an extremal result of the simple integration on parition, never really the form of parition. The basic properties mentioned already, are satisfied by Riemann integration also.

It also follows that, the $max$ and $min$ operations given two functions, preserve the Riemann-integrability. This immediately says, the absolute value of a function also preserves integrability. Similarly, products of to functions also preserve integrability.

Two proof ideas

There are two proof ideas which are worth internalizing. One is the from the basic properties and the other occur in the proof of max,min or product preserving the integrability. These are examples of proofs, where we use proceed from scratch and core definition of integration. Later proofs rely on these important conclusions.

Integrability

So, far we have developed the notion of integration on bounded functions defined on bounded intervals. We saw pieccewise constant functions to be the most basic class of examples which the Riemann integrability is built on top of.

There are two important class of functions that are Riemann-integrable. Ones which are suitably continous, and ones which are suitably monotone. By suitable we mostly mean the functions to be bounded, since that’s the primary requirement for discussing integration in our context. What we are going to see now, is boundedness manifested in various forms revealing different classes of integrable functions.

Continous functions

The first form is a uniformly continous function.

An uniformly continous function $f$ defined on a bounded interval $I$ is Riemann integrable.

These are indeed bounded as we have seen in the earlier article. We write the difference in upper and lower Rieman integrals less than or equal to difference in the upper and lower sums. And the role of uniform continuity is to rather succinctly to describe the difference $\left( sup f(x) - inf f(y) \right) $ which is suppressed in an $\epsilon$ for any $\left| x-y \right| \le \delta$. When we choose a partition $\mathbf{P}$ of cardinality $N$ with length of each interval to be $\left| I \right| / N < \delta$, things follow in order and supress the difference in the upper and lower integrals to zero!

A simple corollary of the above gives us another class. Continous functions on closed intervals are uniformly conitnous!

A continous function $f$ on a closed interval $[a,b]$ is Riemann intgerable.

And infact, with continuity all we require is boundedness!

A continous and bounded function $f$ defined on a bounded interval $I$ is Riemann integrable.

This builds on top of the last corollary. For a small number $\epsilon$, $f$ restricted to $\left[ a-\epsilon,b+\epsilon \right] $ is uniformly continous, so it is integrable. In particular, there is a piecewise constant integral on $\left[ a-\epsilon,b+\epsilon \right] $ close to $\int_{\left[ a-\epsilon,b+\epsilon \right] } f$ by an $\epsilon.$ Let this be given by a p.c function $h$. We may extend this p.c. function to $\tilde{h}$ on the rest of $I$ by defining it to be $M$, the upper bound of $f$ in I, so that $\tilde{h}$ majorizes $f$ in $I$ and $$ \int_I \tilde{h} = \varepsilon M + \int_{[a+\varepsilon,b-\varepsilon]} h + \varepsilon M \leq \int_{[a+\varepsilon,b-\varepsilon]} f + (2M+1)\varepsilon. $$ Now, $$ \overline{\int_I} f \leq \int_{[a+\varepsilon,b-\varepsilon]} f + (2M+1)\varepsilon. $$ The same analysis holds for the lower integral to give an $\epsilon$ supressing difference in both the integrals, proving the integrability!

To summarize, continous bounded functions are integrable because their integrability in closed subintervals and boundedness elsewhere, supress the difference in upper and lower integrals! The integral elsewhere contributes ever so slightly ($\sim\epsilon M$ )and the integral difference on closed sub-interval takes care of the rest.

In fact we don’t require continuity on whole of $I$, it suffices for a function to be piecewise continous (and bounded of course) for integrability!

A piecewise continous and bounded function $F$ defined on a bounded interval $I$ is Riemann integrable.

We can split the function into its partitions on which they are continous and bounded. Each function then is integrable from the last result and the basic property (g) of Riemann integration. An induction then gives that the sum of these functions is also integrable! $$ F(x) = \sum_{i = 1}^{N}F_i(x) $$ where each $F_i$ is defined to be $$ F_i(x) = \begin{cases} F\vert_{J_i}(x) & x\in J_i \\ 0 & x\not\in J_i \end{cases} $$ each $J_i \in \mathbf{P}$, the partition with respect to which the function $F$ is piecewise continous.

That sums up the class of continous functions which are Riemann integrable.

Monotone functions

When we think of monotone functions which are Riemann integrable, we almost immediately go to piecewise continous functions. But we do know from the earlier article that there exist functions which are not necessarily piecewise continous! This is actually wild, because you have on all sub-intervals the function is discontinous\ldots There is a dense discontinuity in some sense. Refer to the article on continuity for the explicit details of an example.

However, it turns out nicely that monotones are integrable provided they are bounded.

A monotone function $f$ is integrable on a closed interval $[a,b]$.

Such a monotone has to be bounded on a closed interval, as we have already seen. The result follows because, the supremum and infimum are very simple for a monotone, in any given interval. It's just a matter of taking (and enumerating) a suitable parition which minimizes the length of intervals, say $(b-a) /N$ for some arbitrary $N$! The difference in upper and lower integrals then gets supressed due to the sum being a telescopic series only depending on $f(b) - f(a)$ and the length $\left( b-a \right) /N $ finally.

We can replace the closed interval with just a bounded interval by further asking the function to be bounded.

A monotone and bounded function $f$ is integrable on a bounded interval $I.$

we can repeat the calculation from the continuity case. Take a closed subinterval, smaller than $I$ by a small number $\sim\epsilon$. $f$ is integrable on this, and we can extend a p.c. function to $I$. The results follows similarly.

This also helps us to give an integral convergence test for an infinite series with a montone descreasing sequence.

Let $f:[0,\infty) \to \mathbb{R}$ be a monotone descreasing function which is non-negative. Then the sum $\sum_{n=0}^\infty f(n)$ is convergent if and only if $sup_{N>0} \int_{[0,N]} f$ is finite.

[to be appreciated\ldots]

A bounded function can be non-integrable. An example is the following. It of course needs to be neither a monotone nor a continous function.

Let $f:[0,1]\to \mathbb{R}$ be the discontinous function $$ f(x) = \begin{cases} 1 & x\in \mathbb{Q} \\ 0 & x \not\in \mathbb{Q}. \end{cases} $$ Then $f$ is bounded but not Riemann integrable.

This follows because $inf\left( f\left( x \right) \right) $ and $sup\left( f\left( x \right) \right) $ in any sub-interval of $[0,1]$ is $0$ and $1$ respectively. So the upper and lower integrals (taking supremum, infimum of the sums) do not match!

We can generalize the Riemann integral slightly further by varying the notion of lengths of intervals. This will in particular be rewarding, when we discuss the effect on the Riemann integration by a change of variable. It also gives us a motivation for the usual notation: $\int_I f dx$!

Part III: Riemann-Stieltjes Integral

We begin with the notion of $\alpha$-length of a bounded interval $I$. The function $\alpha:X\to \mathbb{R}$ is monotone increasing on an interval $X$ that is closed and contains $I$. The following illustration pretty much summarizes the defintion of this new length! 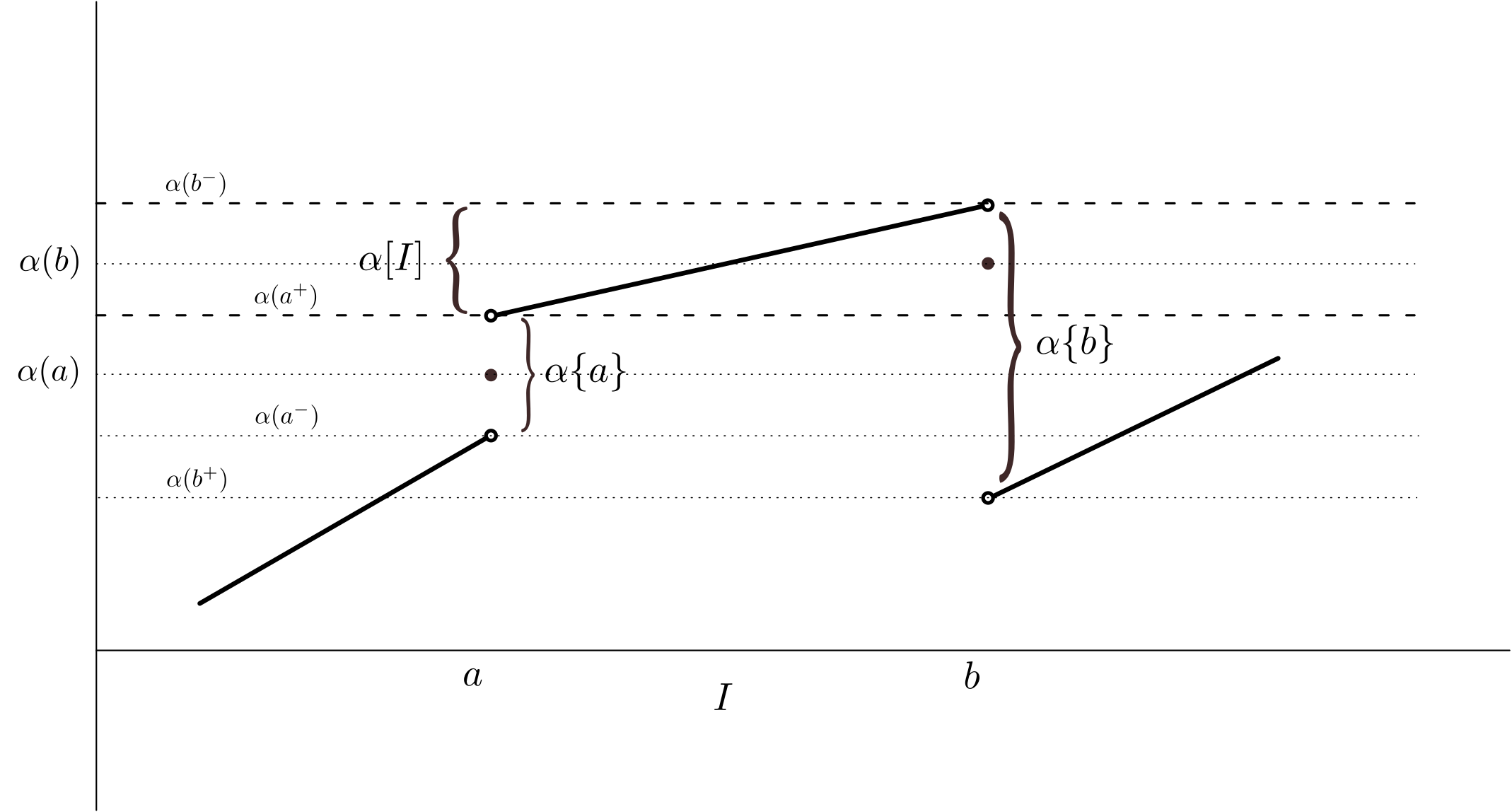If $\alpha$ is however continous on $I \subset X$ then the length is simply, $\alpha[I] = \alpha(b) - \alpha(a).$

Again, the finite additive nature of the usual length follows here. And with an obvious generalization, $p.c. \int_{[P]} f d\alpha = \sum_{J \in \mathbf{P}} c_J\alpha[J]$ also makes sense to define $p.c. \int_I f d\alpha$ which doesn’t depend on the choice of parition! The basics properties of p.c. integral also follow. Riemann-Stieltjes integrability then is an immediate generalization of Riemann integrability where the upper and lower integrals are defined using the p.c. integrals with $\alpha$-lengths instead.

As an interesting remark, when $\alpha(x) = x$, the Riemann-Stieltjes integral is identical to the Riemann integral and we often write, $\int_I f \equiv \int_I f dx \equiv \int_I f(x) dx.$

The class of uniformly continous functions on bounded intervals are still Riemann-Stieltjes integrable but other results may break down when $\alpha$ is discontinous. For example the basic property $(g)$ and the continous bounded class of functions.

[Need to explore this further $\ldots$]

Part IV: Two Fundamental Theorems of Calculus

We can now relate the two pillars of calculus.

Let $f:\left[ a,b \right] \to \mathbb{R}$ be a Riemann integrable function. Let $F:\left[ a,b \right] \to \mathbb{R}$ be the function $$ F(x) := \int_{\left[ a,b \right] } f.$$ Then $F$ is continous. Furthermore, if $x_0 \in \left[ a,b \right]$ and $f$ is continous at $x_0$, then $F$ is differentiable at $x_0$, and $F'(x_0) = f(x_0).$

Coming soon.

In simpler and loose words, the Riemann integral of a function $f$ is itself a continous function. Furthermore when $f$ is continous, it reverts back to $f$ upon differentiation! This precisely encodes the dual nature of integration and differentiation. There is a second part of this story. If the above theorem tells how differentiation of an integral recovers the function, the following gives the commuting picture of how integral of a derivative recovers the original function.

Let $f:\left[ a,b \right] \to \mathbb{R}$ be a Riemann integrable function. And $F:\left[ a,b \right] \to \mathbb{R}$ is an anti-derivative of $f$, i.e. $F$ is differentiable everywhere and $F'(x) = f(x)$ for all limit points $x \in \left[ a,b \right]$. Then, $$ \int_{\left[ a,b \right] } f = F(b) - F(a).$$

Coming soon.

This simply means $\int_{\left[ a,b \right]} F’ = F(b) -F(a).$ If $f$ is continous, then from the first theorem there is an anti-derivative of $f$ on $\left[ a,b \right] $ and recovers $f$ on integration. This existence of anti-derivative and then integrating to recover the function is precisely the combined content of the above two theorems.

However, we should note the subtleties that exist –

The first theorem $f$ only has a local anti-derivative depending on its continuity. That is, the duality holds under certain restrictions.
The risk of writing $\int_{\left[ a,b \right]} F’ = F(b) - F(a)$ is that $F’$ need not be Riemann integrable for any function $F$. And the above theorem states in a way that takes cares of this by demanding Riemann integrability of a function and then assuming there’s an anti-derivative. That is, the duality again holds under certain restrictions.

For example, consider the function

\[\begin{align*} F:\left[ -1,1 \right] &\to \mathbb{R} \\ F(x) &= \begin{cases} x^2\sin\left( \frac{1}{x^3} \right) & x \neq 0 \\ 0 & x = 0. \end{cases} \end{align*}\]

which is differentiable everywhere, but the derivative $F’$ is unbounded and thus not Riemann integrable!

But these restrictions are indeed simple. A continous $f$ readily uses both the full potential of the two theorems!

To get the full feel of why this magic duality holds, analyse the above proofs [coming soon.]

We should also note that there is an ambiguity in the anti-derivative of a function. This manifests as a difference by a constant function. Of course, by anti-derivative we mean indefinite integrals and the constant is the $+C$ integration factor!

Applications of Fundamental theorems

There are two main consequences of the above theorems. One is the integration by parts and the other is the effect of integrals due to a change of variable. The path we are going to take also reveals the remarkable interaction between the Riemann-Stieltjes and Riemann integrals!

(Integration by parts formula). Let $I = [a, b]$, and let $F : [a, b] \to \mathbf{R}$ and $G : [a, b] \to \mathbf{R}$ be differentiable functions on $[a, b]$ such that $F'$ and $G'$ are Riemann integrable on $I$. Then we have $$ \int_{[a, b]} FG' = F(b)G(b) - F(a)G(a) - \int_{[a, b]} F'G. $$

Let $\alpha : [a,b] \to \mathbf{R}$ be a monotone increasing function, and suppose that $\alpha$ is also differentiable on $[a,b]$, with $\alpha'$ being Riemann integrable. Let $f : [a,b] \to \mathbf{R}$ be a function which is Riemann-Stieltjes integrable with respect to $\alpha$ on $[a,b]$. Then $f\alpha'$ is Riemann integrable on $[a,b]$, and $$ \int_{[a,b]} f\,d\alpha = \int_{[a,b]} f\alpha'. $$

With this, we have two version of change of variables formula, one with Riemann-Stieltjes type and other just the Riemann type.

Let $[a, b]$ be a closed interval, and let $\phi : [a, b] \to [\phi(a), \phi(b)]$ be a continuous monotone increasing function. Let $f : [\phi(a), \phi(b)] \to \mathbf{R}$ be a Riemann integrable function on $[\phi(a), \phi(b)]$. Then $f \circ \phi : [a, b] \to \mathbf{R}$ is Riemann-Stieltjes integrable with respect to $\phi$ on $[a, b]$, and $$ \int_{[a,b]} f \circ \phi\,d\phi = \int_{[\phi(a),\phi(b)]} f. $$

Let $[a,b]$ be a closed interval, and let $\phi : [a,b] \to [\phi(a), \phi(b)]$ be a differentiable monotone increasing function such that $\phi'$ is Riemann integrable. Let $f : [\phi(a), \phi(b)] \to \mathbf{R}$ be a Riemann integrable function on $[\phi(a), \phi(b)]$. Then $(f \circ \phi)\phi' : [a,b] \to \mathbf{R}$ is Riemann integrable on $[a,b]$, and $$ \int_{[a,b]} (f \circ \phi)\phi' = \int_{[\phi(a),\phi(b)]} f. $$

There is another notion of integration which applies to a larger class of functions – the Lesbegue integration. Which shall occupy our study in second part of Analysis.